Introduction to integral : Definition, Types, and examples.

Definition of integral :

“In mathematics, an integral assigns numbers to functions in a way that defines the area, displacement, volume, and other concepts that arise by joining the infinitely small data.”

Notation :

The notation of integral has two types. One is used for indefinite integrals and the other is used for definite integrals.

Explanation :

* ∫ integral symbol

* F(x) is the integrand

* dx is the differential of x

* a, b are the lower and upper limits respectively.

Types of integral

There are many types of integrals in mathematics. Further in this article, we will just discuss the two basic types of integrals :

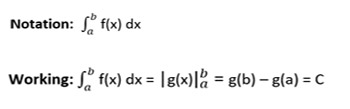
1. Indefinite integral : It is the type of integration that doesn’t have any boundary values.

Notation : ∫ f(x) dx
Working : ∫f(x) dx = g(x) + c

* g(x) + c is the answer.

* Where c is any constant which is added to the result.

2. Definite integral : The definite integral is the type of integrals that are bounded. This type of integral contains lower and upper limits.
Integration

* a, b are the upper and lower bounds respectively.

* C is the result.

Rules of integral

In pre-calculus integrals, we use some rules to solve them and make the calculations easier. The rules are given below in the table.

Integration

Examples of integral

Examples are the most important part of any topic it helps us to understand the concepts more clearly.

Example 1 : For indefinite integral

Evaluate the integration of 10x⁴ + 6sin(x) – 12x⁵y³ + 2xy w.r.t “x”.

Solution:

Step 1: Apply the integral to the function.

ʃ (10x⁴ + 6sin(x) – 12x⁵y³ + 2xy) dx

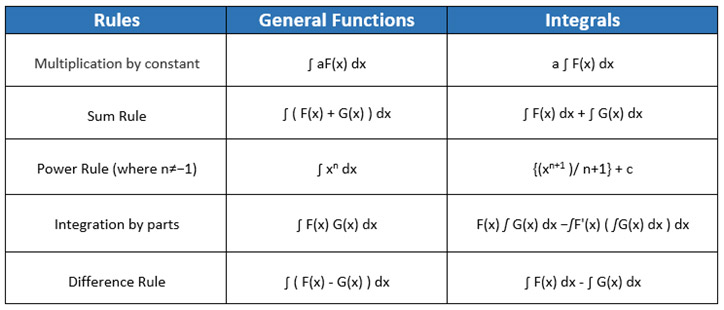
Step 2: Separate the integrals using the sum rule.

ʃ (10x⁴ + 6sin(x) – 12x⁵y³ + 2xy) dx = ʃ (10x⁴) dx + ʃ 6sin(x) dx – ʃ 12x⁵y³ dx + ʃ 2xy dx

Step 3: Apply multiplication by constant rule and write the constants outside of the integrals.

ʃ (10x⁴ + 6sin(x) – 12x⁵y³ + 2xy) dx = 10 ʃ (x⁴) dx + 6 ʃ sin(x) dx – 12 y³ʃ x⁵ dx + 2y ʃ x dx

Step 4: Simplify.

ʃ (10x⁴ + 6sin(x) – 12x⁵y³ + 2xy) dx = 10 (x⁴⁺¹ / 4 + 1) + 6 (– cos(x)) – 12y³(x⁵⁺¹ / 5 + 1) + 2y (x¹⁺¹ / 1 + 1) + C

= 10 (x⁵ / 5) – 6 (cos(x)) – 12y³(x⁶ / 6) + 2y (x² / 2) + C

= 10/5 (x⁵) – 6 (cos(x)) – (x⁶) 12y³/ 6 + 2y (x² / 2) + C

= 2 (x⁵) – 6 (cos(x)) – 2y³(x⁶) + y (x²) + C

= 2x⁵ – 6 cos(x) – 2 x⁶y³ + x²y + C

To get rid of these long calculations use an integral calculator. This calculator will give you a step-by-step solution to the integral problems in a couple of seconds.

Example 2: For definite integrals

Integrate 22x⁵ + 3sin(x) – 6x³ + 14x w.r.t x, on the interval [2, 5].

Solution

Step 1: Apply the integral symbol on the function, and write the limits carefully.

Integrals

Step 2: Apply the sum rule.

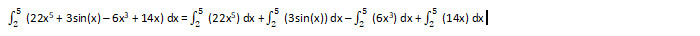
Step 3: Write the constants outside the integrals using the constant multiplication rule.

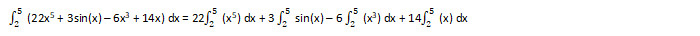
Integrals

Step 4: Simplify.

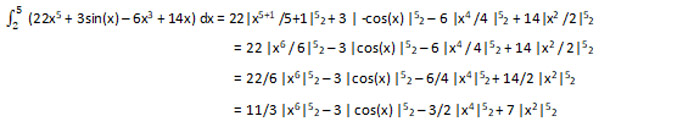
Integrals

Step 5: Put the limits in the variable x.
Integrals

Summary : In this article, we studied the definition of integral and types of integrals along with examples. Now you are witnessed that integration is not a difficult topic. After reading this article you can solve the pre-calculus integrals easily.